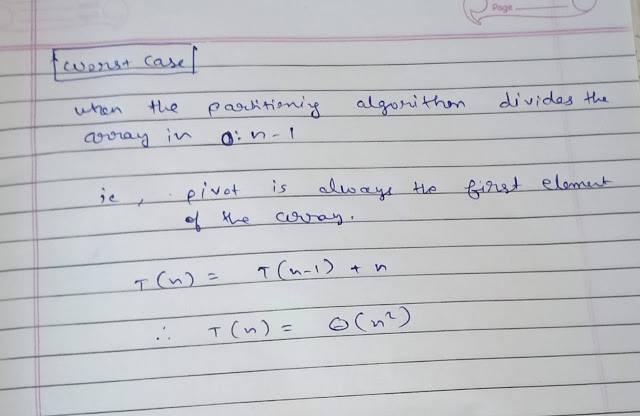Sunday, 27 March 2022
The QuickSelect Algorithm
Tuesday, 15 March 2022
Primality Test
What is Primality test?
Primality test is an algorithm used to determine if a number is prime or not.
One of the basic algorithm used is given below:
Its time complexity is O(√n), and space complexity is O(1).
Suppose n is greater than 10^20 ie out of range of the long long int , the largest container of c++ in terms of size(8 bytes).
In this case the mentioned algo will indeed perform poorly. Therefore we must have some techinque/algorithm to counter bigger numbers.
Sieve of Eratosthenes
Why is this algorithm efficient?
One of the best algorithm to check if a number is prime or not is given below:
The time complexity of this algorithm is O(√n), here 'n' is the number under consideration. Suppose we have a total of 'Q' numbers , Q and n can be as large as a million. Now we have to check each number whether it is prime or not.
Since, n and Q are the order of 10^6, therefore in worst case, our machine would have to do O(Q√n) computations ie ~10^6*10^3=10^9 computations, which will take more than the expected time!
Here comes this Sieve algorithm. It is a preprocessing technique which generates all the prime numbers between 0 and a given limit. It is very efficient in cases we have to find all the prime numbers between a range.
Auxiliary Space O(n)
Implementation of the algorithm using C++