Flood Fill Algorithm
Flood fill algorithm helps in visiting each and every point in a given area. It determines the area connected to a given cell in a multi-dimensional array. Following are some famous implementations of flood fill algorithm:
Bucket Fill in Paint:
Clicking in an area with this tool selected fills that area with the selected color.
Solving a Maze:
Given a matrix with some starting point, and some destination with some obstacles in between, this algorithm helps to find out the path from source to destination
Minesweeper:
When a blank cell is discovered, this algorithm helps in revealing neighboring cells. This step is done recursively till cells having numbers are discovered.
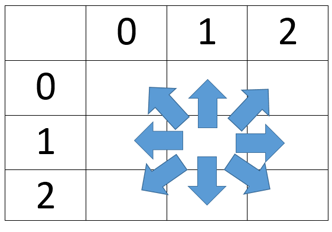
Flood fill algorithm can be simply modeled as graph traversal problem, representing the given area as a matrix and considering every cell of that matrix as a vertex that is connected to points above it, below it, to right of it, and to left of it and in case of 8-connections, to the points at both diagonals also. For example, consider the image given below.
function DFS(x, y, visited, n, m)
if (x ≥ n OR y ≥ m)
return
if(x < 0 OR y < 0)
return
if(visisted[x][y] == True)
return
visited[x][y] = True
DFS(x-1, y-1, visited, n, m)
DFS(x-1, y, visited, n, m)
DFS(x-1, y+1, visited, n, m)
DFS(x, y-1, visited, n, m)
DFS(x, y+1, visited, n, m)
DFS(x+1, y-1, visited, n, m)
DFS(x+1, y, visited, n, m)
DFS(x+1, y+1, visited, n, m)